EQUATIONS DU PREMIER DEGRE A UNE INCONNUE

II. EQUATIONS REDUCTIBLES AU PREMIER DEGRE

II.1 EQUATIONS PRODUITS \(A.B.C…=0\)

Soit à résoudre l’équation \(A.B.C=0\) )où A, B et C sont des facteurs du premier degré, on utilise la propriété suivante : \(A.B.C…=0 \ \Leftrightarrow \ (A=0) \; ou \; (B=0)ou (C=0)…\)

Exemple 5

Résoudre \((2x-3)(4x-1)(x-4)(-2x+8)=0\)
\(\Leftrightarrow 2x-3=0 \; ou \; 4x-1=0 \; ou \; x-4=0 \; ou\; -2x+8=0\)
\(\Leftrightarrow 2x=3 \ ou\ 4x=1 \ ou\ x=4 \ ou\ -2x=-8\)
\(\Leftrightarrow x=\frac{3}{2} ou x=\frac{1}{4} ou x=4 ou -x=\frac{-8}{-2}\)
\(\Leftrightarrow x=\frac{3}{2} \ ou\ x=\frac{1}{4} \ ou\ x=4 \ ou \ x=4\)
\(S=\{\frac{3}{2}, \ \frac{1}{4} \ , 4 \}\)

Remarque

Même les équations de degré supérieur à 1 peuvent être ramenées sous cette forme par décomposition ou factorisation.

Exemple 6

Résoudre \(x^2-5x+6=0\)

Décomposons le trinôme donné. Il y a plusieurs méthodes pour le faire, mais voici celle que nous allons utiliser : Soit \(P(x)=x^2-5x+6\)

Trouver les diviseurs du terme indépendant

Dans notre cas, le terme indépendant c’est 6 et ses diviseurs sont : \( \pm 1,\ ; \pm2\ ; \pm 3 \ et \ \pm 6\)
Remplacer les diviseurs dans le polynôme et retenir celui qui annule le polynôme, c’est-à-dire, soit \(x_{0}\), tel que \(x_{0}\) est diviseur du terme indépendant, calculer \(P(x_{0})\) et retenir celui pour lequel \(P(x_{0})=0\).

Pour notre exemple : Pour -1 ∶ \(P(-1)=(-1)^2-5(-1)+6=12\neq0\) à rejeter
Pour 1 ∶ \(P(1)=(1)^2-5(1)+6=2\neq 0\) à rejeter
Pour 2 ∶ \(P(2)=(2)^2-5(2)+6=0\) à considérer
Inutile de tester les autres diviseurs car on a déjà trouvé un qui vérifie :

Effectuer la division de \(P(x) \: par \; x-x_{0},\: x_{0}\) étant le diviseur qui a vérifié la condition prétendante.

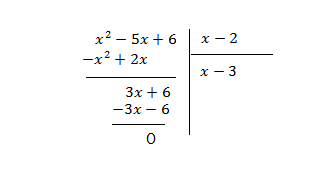Le polynôme sera égal au produit du diviseur et du quotient :

\(x^2-5x+6 \Leftrightarrow(x-2)(x-3)\)
\(\Rightarrow x^2-5x+6=0 \Leftrightarrow (x-2)(x-3)=0\)
\(\Leftrightarrow x-2=0 \ ou \ x-3=0\)
\(\Leftrightarrow x=2 \ ou\ x=3\)
\(S=\{2;3\}\)

Exemple 7

Résoudre : \(x^3-6x^2+3x+10=0\)
Décomposons \(x^3-6x^2+3x+10\)
Les diviseurs de 10 sont : \(\pm1\ ;\ \pm2 \ ;\ \pm5 \ et \ \pm10\)
Parmi ces diviseurs, -1 annule le polynôme
Effectuons la division de \(x^3-6x^2+3x+10 \ par\ x+1\)
oups

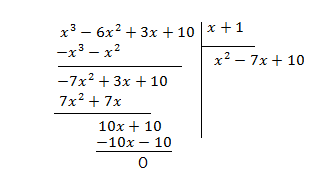
\(x^3-6x^2+3x+10\Leftrightarrow (x+1)(x^2-7x+10)\)
On constate qu’après décomposition, il y a un facteur, qui n’est pas du premier degré, nous devons le décomposer à son tour.
\(x^2-7x+10\)
Parmi les diviseurs de 10, il y a 2 qui annule le trinôme, effectuons la division de \(x^2-7x+10 \ par\ x-2\)
oups

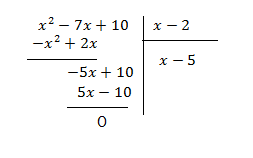
\(x^3-6x^2+3x+10 \Leftrightarrow (x+1)(x^2-7x+10)\)
\(Or\ x^2-7x+10 \Leftrightarrow (x-2)(x-5)\)
\(\Leftrightarrow x^3-6x^2+3x +10\Leftrightarrow(x+1)(x-2)(x-5)\)
\(\Leftrightarrow x+1=0 \ ou\ x-2=0 ou x=5\)
\(\Leftrightarrow x=-1 \ ou \ x=2 \ ou\ x=5\)
\(S=\{-1\ ;\ 2\ ;\ 5\}\)

II.2. EQUATIONS FRACTIONNAIRES

Une équation du premier degré est dite fractionnaire si un dénominateur au moins contient une inconnue.

Résolution

Pour résoudre une équation fractionnaire, on procède comme suit :

Poser les conditions préalables sur les dénominateurs
Résoudre l’équation
Retenir que les valeurs de l’inconnue qui vérifient la condition préalable

Exemple 8

Résoudre : \(\frac{2}{x-4}+\frac{3}{x-2}=\frac{5}{x+1}\)
Condition préalable :\( x-4\neq 0 \ et\ x-2\neq0 \ et \ x+1\neq 0\)
\(\Leftrightarrow x\neq 4 \ et \ x\neq 2 \ et\ x\neq -1\)
C’est-à-dire si nous trouvons 4, 2 ou -1 comme solution, il faut le rejeter.
Résolvons l’équation
\(\frac{2}{x-4}+\frac{3}{x-2}=\frac{5}{x+1}\)
\(\Leftrightarrow \frac{2}{x-4}+\frac{3}{x-2}-\frac{5}{x+1}=0\)
\(\Leftrightarrow \frac{2(x-2)(x+1)+3(x-4)(x+1)-5(x-4)(x-2)}{ (x-4)(x-2)(x+1)}=0\)
\(\Leftrightarrow \frac {2(x^2+x-2x-2)+3(x^2+x-4x-4)-5(x^2-2x-4x+8)}{ (x-4)(x-2)(x+1)}=0\)
\(\Leftrightarrow \frac {2(x^2-x-2)+3(x^2-3x-4)-5(x^2-6x+8)}{ (x-4)(x-2)(x+1)}=0\)
\(\Leftrightarrow \frac {2x^2-2x-4+3x^2-9x-12-5x^2+30x-40}{ (x-4)(x-2)(x+1)}=0\)
\(\Leftrightarrow 2x^2-2x-4+3x^2-9x-12-5x^2+30x-40=0\)
\(\Leftrightarrow (2x^2+3x^2-5x^2 )+(-2x-9x+30x)+(-4-12-40)=0\)
\(\Leftrightarrow 19x-56=0\)
\(\Leftrightarrow 19x=56\)
\(\Leftrightarrow x=\frac{56}{19}\)
\(S=\{\frac{56}{19}\}\)

Exemple 9

Résoudre :\(\frac{7}{7x-1}-\frac{2}{x+1}=\frac{1}{7x-1}\)
Condition préalable : \(7x-1\neq 0\ et \ x+1\neq 0\)
\(\Leftrightarrow x\neq \frac {1}{7 } \ et \ x\neq -1\)
Résolvons l’équation
\(\frac{7}{7x-1}-\frac{2}{x+1}=\frac{1}{7x-1}\)
\(\Leftrightarrow \frac{7}{7x-1}-\frac{2}{x+1} - \frac{1}{7x-1}=0\)
\(\Leftrightarrow \frac {7(x+1)-2(7x-1)-1(x+1)}{(7x-1)(x+1)}=0\)
\(\Leftrightarrow (7(x+1)-2(7x-1)-1(x+1)) =0\)
\(\Leftrightarrow (7x+7-14x+2-x-1) =0 \)
\(\Leftrightarrow 7x+7-14x+2-x-1=0\)
\(\Leftrightarrow (7x-14x-x)+(7+2-1)=0\)
\(\Leftrightarrow -8x+8=0\)
\(\Leftrightarrow -8x=-8\)
\(\Leftrightarrow x=1\)
\(S=\{1\}\)

II.3 EQUATIONS CONTENANT DES VALEURS ABSOLUES

On sait que \(\|a\|\ =\ \left\{ \begin{array}{r c l} a \ si\ a\geq 0\\ -a \ si\ a\leq 0 \end{array} \right. \)

Exemple 10

Résoudre :
\(|5x-3|=12\)
Par définition de la valeur absolue :
\(|5x-3|=\left\{ \begin{array}{r c l} 5x-3 \ si\ 5x-3\geq 0\\ -(5x-3) \ si\ 5x-3\leq 0 \end{array} \right. \)
\(=\left\{ \begin{array}{r c l} 5x-3 \ si\ 5x\geq 3\\ -(5x-3) \ si\ 5x\leq 3 \end{array} \right. \)
\(|5x-3|=\left\{ \begin{array}{r c l} 5x-3 \ si\ x\geq \frac{3}{5}\\ -(5x-3) \ si\ x\leq \frac{3}{5} \end{array} \right. \)
equations du premier degré

\(|5x-3|\) a deux valeurs selon que \(x\geq \frac{3}{5} \;ou\; x\leq \frac{3}{5}\)
Examinons les deux cas :
Si \(x\geq \frac{3}{5} \Leftrightarrow x\in [\frac{3}{5}; +\infty[ :\) la valeur de \(|5x-3|\ vaut\ 5x-3\), en remplaçant cette valeur dans l’équation initiale à la place de \(|5x-3|\) , on a :
\(5x-3=12 \Leftrightarrow 5x=12+3\)
\(\Leftrightarrow 5x=15\)
\( \Leftrightarrow x=\frac{15}{5}\)
\(S_{1}={3}\)
Si \(x\leq \frac{3}{5} \Leftrightarrow x\in ]-\infty;\frac{3}{5} ]\) : la valeur de \(|5x-3|\; vaut 3-5x\),en remplaçant cette valeur à la place de \(|5x-3|\) dans l’équation initiale, on a :
\(3-5x=12 \Leftrightarrow -5x=12-3\)
\(\Leftrightarrow -5x=9\)
\(\Leftrightarrow -x=\frac{9}{5}\)
\(S_{2}=\{\frac{-9}{5}\}\)
\(S=S_{1}\cup S_{2}\)
\(S=\{\frac{-9}{5};3\}\)

Exemple 11

Résoudre : \(|x-5|-2=|2x+3|\)
\(|x-5|= \left\{ \begin{array}{r c l} x-5 \ si\ x-5\geq 0\\ -(x-5) \ si\ x-5\leq 0 \end{array} \right. \)
\( = \left\{ \begin{array}{r c l} x-5 \ si\ x\geq 5\\ 5-x \ si\ x\leq 5 \end{array} \right. \)
\(|2x+3|= \left\{ \begin{array}{r c l} 2x+3 \ si\ 2x+3\geq 0\\ -(2x+3) \ si\ 2x+3\leq 0 \end{array} \right. \)
\(=\left\{ \begin{array}{r c l} 2x+3 \ si\ 2x\geq -3\\ -(2x+3) \ si\ 2x\leq -3 \end{array} \right. \)
\(=\left\{ \begin{array}{r c l} 2x+3 \ si\ x\geq \frac{-3}{2}\\ -2x-3 \ si\ x\leq \frac{-3}{2} \end{array} \right. \)
equations du premier degré

La droite numérique \(\mathbb {R}\) est divisé en 3 parties :
\(]-\infty; \frac{-3}{2}] \; [\frac{-3}{2};5]\ et \ [5; +\infty[\)

On va examiner les trois cas en remplaçant à chaque fois l’expression entre signe valeur absolue par sa valeur correspondante dans l’intervalle considéré.

Pour \(x \in ]-\infty; \frac{-3}{2}] ∶5-x-2=-2x-3\)
\(\Leftrightarrow -x+2x=-3-5+2\)
\(\Leftrightarrow x=-6\)
\(S_{1}=\{-6\}\)
Pour \(x \in [\frac{-3}{2};5]: 5-x-2=2x+3\)
\(\Leftrightarrow -x-2x=3+2-5\)
\(\Leftrightarrow -3x=0\)
\(\Leftrightarrow -x=\frac{0}{3}\)
\(S_{2}={0}\)
Pour \(x \in [5; +\infty[:x-5-2=2x+3\)
\(\Leftrightarrow x-2x=3+2+5\)
\(\Leftrightarrow -x=10\)
\(\Leftrightarrow x=-10 \: \; à rejeter \; car -10 \notin[5; +\infty[\)
\( S_{3}=\varnothing\)
\(S=S_{1}\cup S_{2}\cup S_{3}\)
\(S=\{-6,0\}\)

Retrouvez ce cours en format pdf
Télécharger

Retrouvez ce cours en format pdf
Télécharger