I. EQUATIONS DU SECOND DEGRE

I. EQUATIONS DU SECOND DEGRE

I.1 DEFINITIONS

I.1 DEFINITIONS

Commençons en douceur pour ne pas faire mal aux autres…

Dans cette section, nous allons essayer d’expliquer ce que signifie une équation et nous verrons aussi ce quoi une équation du second degré

I.1.1 Equation

I.1.1 Equation

Une équation est une égalité qui comporte au moins une inconnue.

Une inconnue est représentée par une lettre remplaçant un nombre dont on ne connait pas sa valeur.

Exemple : \(2x+3=5 \; ; x+2y=5\; et \; x^2-5x+6=0\) sont des équations.
Contre-exemple : \(56=50+6\) n’est pas une équation : c’est une égalité vraie mais qui n’a pas des inconnues.

\(2x+4\) N’est pas une équation car il n’y a pas d’égalité quoiqu’ayant une inconnue.

I..1.2 Equation à une inconnue

I..1.2 Equation à une inconnue

Une équation est dite à une inconnue si elle ne comporte qu’une seule inconnue (variable). Sachez que l’inconnue (la lettre) peut se répéter plusieurs fois.

Exemple : \(2x+3=4x+6 \; ; \; x^2+5x+6=0 \; ; \; x^3+25x^2+30=0 \) sont des équations à une variable.

Contre-exemple : \(2x+3y=4\) n’est pas une équation à une inconnue car elle comporte deux inconnues ( x et y)

I.1.3 Equation du second degré

I.1.3 Equation du second degré

Une équation est dite du second degré lorsque le degré supérieur de l’inconnue est deux. En d’autres termes, une équation du second degré est une équation dont l’exposant le plus élevé de l’inconnue est 2.

Exemple : \(x^2-5x+6=0 \; ; \; x^2-9x+6=0 \; ; \; 2x+3-2x^2=0 \) sont des équations du second degré.

Contre-exemple : \(2x+3=0 ; x^3+2x^2=3 ;2x+4=5x+7\) ne sont des équations du second degré.

I.2 RESOLUTION

I.2 RESOLUTION

Maintenant que vous savez ce qui signifie une équation du second degré, voyons maintenant comment résoudre ça.

Une équation du second degré en x a la forme générale ci-après :
\(ax^2+bx+c=0 \quad Avec \quad a \in \mathbb{R^*} \quad ;b,c \in \mathbb{R} \)

a, b et c sont les coefficients :

• \(a \) est le coefficient de \(x^2\), en d’autres termes, a est le nombre devant \(x^2\) et cela qu’il soit au milieu, à la fin ou au début de l’équation.
• \(b \) est le coefficient de \(x \). Si ce n’est pas clair, sachez que b est le nombre qui se trouve devant \(x \).
• \(c\) est le terme indépendant, c’est-à-dire le nombre qui n’est pas accompagné de \(x \; ou \; x^2 \)

Je crois que ça sera plus clair avec des exemples :

\(x^2-5x+6=0\) , pour cette équation : \(a=1; b=-5 \; et \; c=6\)

\(-2x^2+5x-3=0\), pour celle-ci : \(a=-2 ;b=5 \; et \; c=-3 \)

\(6-9x+x^2=0 \quad : \quad a=1 ;b= -9 \; et \; c=6 \)

\(x^2-1=0 \quad : \quad a=1 ;b=0 \; et \; c=-1\)

I.2.1 Cas général

I.2.1 Cas général

Pour résoudre une équation ayant la forme général \(ax^2+bx+c=0\), on procède comme suit :

• D’abord, on identifie les valeurs de a, b et c
• - Ensuite, on calcule le discriminant ou le réalisant (delta) par la formule :
  \( \Delta = b^2-4ac\)

Etant donné que \(\Delta \) est un réel, trois cas sont possibles : il peut être positif \((\Delta>0)\), nul \((\Delta=0)\) ou négatif \((\Delta<0) \). Les solutions dépendent de ces trois cas.

1er cas : Le discriminant est positif \((\Delta>0)\)

1er cas : Le discriminant est positif \((\Delta>0)\)

Dans ce cas, l’équation admet deux racines réelles données par les formules suivantes :

\(x_1=\frac{-b-\sqrt{\Delta}}{2a} \quad et \quad x_2=\frac{-b+\sqrt{\Delta}}{2a} \) Ou sous la forme condensée :

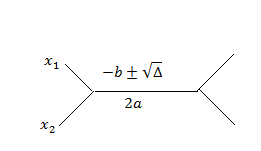
2e cas : Le discriminant est nul \((\Delta=0)\)

2e cas : Le discriminant est nul \((\Delta=0)\)

Dans ce cas, l’équation admet une racine double donnée par la formule :

\(x_1=x_2=\frac{-b}{2a} \)

3e cas : Le discriminant est négatif \((\Delta <0)\)

3e cas : Le discriminant est négatif \((\Delta <0)\)

Si le discriminant est négatif, alors l’équation n’admet pas de racines réelles et par conséquent :\( S=\phi\).

Exemple 1

Exemple 1

Résoudre dans \(\mathbb{R} \) , les équations suivantes :

\( a) x^2-5x+6=0\)

\( b) x^2-6x+9=0\)

\( c) 2x^2+4x+3=0\)

Resolution

\(x^2-5x+6=0\)
\(a=1 ;b=-5 \; et \; c=6 \)

Il suffit de remplacer chaque paramètre par sa valeur dans la formule du discriminant.

\(\Delta=b^2-4ac \)
\(\Delta=(-5)^{2}-4\times 1 \times 6 \)
\( =25-24 \)
\( \Delta=1 >0 \)

Comme le discriminant est positif, nous sommes dans le premier cas : on aura deux racines réelles.

\(S=\{2 ; 3\} \)

Pour lire la suite du cours, veuillez télécharger ce cours en format pdf
Télécharger