

SYSTEMES DE NUMERATION
SYSTEMES DE NUMERATION
Salut.
Dans ce cours, nous allons aborder les systèmes de numération.
N’ayez aucune crainte, même si c’est la première fois que vous étudiez ça, car dans ce cours, on explique le tout de façon très clair pour une bonne compréhension.
A la fin de ce cours, vous serez capable :
- De convertir un nombre d’une base quelconque vers une autre
- D’utiliser l’arithmétique et les fractions en binaire pour convertir de la base décimale vers la base binaire et vice versa.
- D’effectuer les opérations fondamentales (addition, soustraction, multiplication et division) en binaire.
A la fin du cours, nous vous proposons une série d’exercices résolus et non résolus pour votre entrainement.
Si vous avez de questions ou suggestions, n’hésitez pas à me contacter.
Bonne lecture.
INTRODUCTION
INTRODUCTION
Selon Wikipédia, un système de numération est un ensemble de règles d’utilisation des signes permettant d’écrire les nombres.
D’une manière générale, en base N (système N), on a besoin de N chiffres, de \(0 \; à \; N-1\). Chaque chiffre dans ce système peut avoir \(N-1\) valeurs différentes.
Pour la base 2 (binaire) : on a deux chiffres :\( 0 \; et \; 1 \)
Pour la base 3(trinaire) : \(0,1 \; et \; 2 \)
Pour la base 4 :\( 0, 1, 2 \; et \; 3\)
Pour la base 5 : \(0, 1, 2, 3, \; et \; 4\)
Pour la base 6 : \(0,1, 2, 3, 4 \; et \; 5\)
Pour la base 7 : \(0, 1, 2, 3, 4, 5, \; et \; 6\)
Pour la base 8 (octal) : \(0, 1, 2, 3, 4, 5, 6 \; et \; 7\)
Pour la base 9(nonaire) : \(0,1,2, 3, 4, 5, 6, 7 \; et \; 8\)
Pour la base 10 (décimale) :\( 0, 1, 2, 3, 4, 5, 6, 7, 8 \; et \; 9\)
Pour les bases strictement supérieures à 10, on a besoin de l’adjonction (ajout) de nouveaux chiffres, généralement les lettres (A à Z) pour les \(11 \leqslant bases\leqslant 36\)
Par exemple pour la base 16, les chiffres utilisés sont : \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E \; et \; F.\) A représente 10, B représente 11 ainsi de suite.
Pour d’autres cas, on considère les nombres à plus d’un chiffre en base 10 comme de nouveaux chiffres.
Exemple (45;17)_{60} On les sépare par des points virgules pour indiquer qu’il s’agit de chiffres.
I.CONVERSION ENTRE LES BASES
I.CONVERSION ENTRE LES BASES
Dans cette section nous allons voir comment quitter d’une base vers une autre base.
1. Passage de la base décimale vers une autre base (codage)
1. Passage de la base décimale vers une autre base (codage)
a) Cas de nombres entiers
a) Cas de nombres entiers
Pour passer de la décimale vers une autre base, on effectue des divisions successives par la base de destination et conserver les restes successifs comme chiffres de poids croissants du résultat.
Exemple 1
\((57)_{10}=(?)_{2} \)
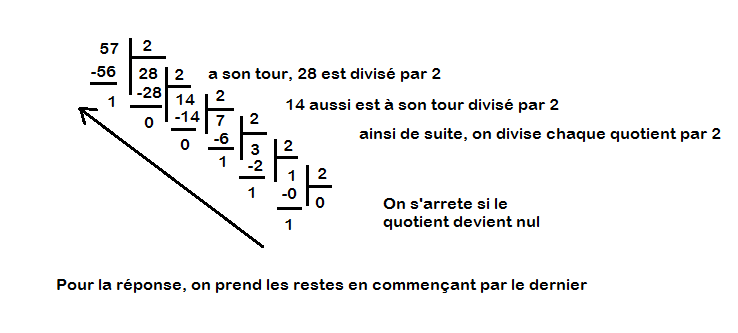
Donc \((57)_{10}=(111001)_{2}\)
Exemple 2
\((345)_{10}=(?)_{8} \)

Donc \((345)_{10}=(531)_{8} \)
Exemple 3
\((495)_{10}=(?)_{16} \)

\((495)_{10}=(1EF)_{16} \)
b) Cas des nombres flottants (avec une virgule)
b) Cas des nombres flottants (avec une virgule)
Lorsque le nombre à convertir comporte une virgule, on procède comme suit :
Séparer la partie entière de la mantisse (partie décimale) :
- Pour la partie entière, procéder comme expliquée ci-haut.
- Pour la mantisse, on procède comme suit :
Effectuer des multiplications successives de la mantisse par la base de destination et conserver les parties entières successives comme chiffres de poids décroissants du résultat.
Exemple 4
\((31,4375)_{10}=(?)_{2} \)

\((31,4375)_{10}=(11111,0111)_{2} \)
Exemple 5
\((0,32275390625)_{10}=(?)_{16} \)
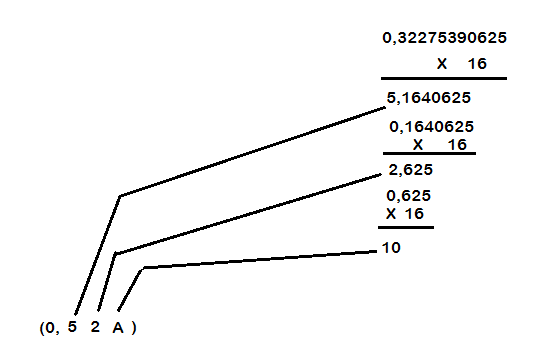
\((0,32275390625)_{10}=(0,52A)_{16} \)
Exemple 6
\((25,589599609375)_{10}=(?)_{8} \)
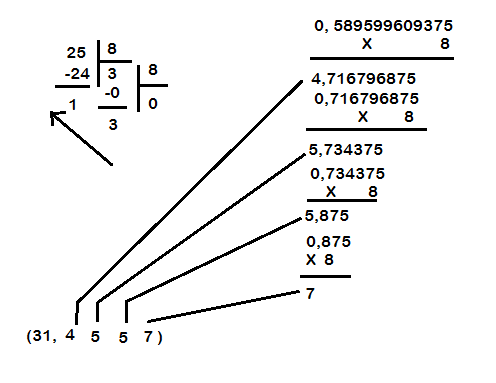
\((25,589599609375)_{10}=(31,4557)_{8} \)
Pour lire la suite du cours, veuillez télécharger le pdf
Télécharger
